Statistische significantie
Statistische significantie drukt de betrouwbaarheid van gemeten gegevens uit, waardoor bedrijven echte effecten van toeval kunnen onderscheiden en weloverwogen ...
Ontdek hoe statistische significantie bepaalt of resultaten echt zijn of toeval. Begrijp p-waarden, hypothesetoetsing en praktische toepassingen voor uw bedrijf in 2025.
Statistische significantie wordt gebruikt om te bepalen of een resultaat op toeval berust of veroorzaakt wordt door een relevante factor. Als het statistisch significant is, is het onwaarschijnlijk dat het door toeval is ontstaan.
Statistische significantie is een fundamenteel begrip in data-analyse waarmee u onderscheid maakt tussen echte effecten en willekeurige schommelingen in uw data. Wanneer u experimenten uitvoert, enquêtes afneemt of bedrijfsstatistieken analyseert, heeft u een betrouwbare methode nodig om te bepalen of de patronen die u ziet echt zijn of simpelweg het resultaat van toeval. Statistische significantie biedt dit kritische kader door wiskundige principes te gebruiken om de kans te beoordelen dat uw waargenomen resultaten zouden optreden als er werkelijk geen effect of verschil is tussen de groepen die u vergelijkt.
Het concept is ontstaan uit het werk van statisticus Ronald Fisher in het begin van de 20e eeuw en is de hoeksteen geworden van hypothesetoetsing in vrijwel elk vakgebied dat afhankelijk is van data-analyse. Van farmaceutisch onderzoek dat nieuwe geneesmiddelen valideert tot e-commercebedrijven die conversieratio’s optimaliseren: statistische significantie fungeert als poortwachter tussen bruikbare inzichten en misleidende conclusies. Begrijpen hoe statistische significantie werkt, stelt u in staat weloverwogen beslissingen te nemen op basis van solide bewijs in plaats van intuïtie of toeval.
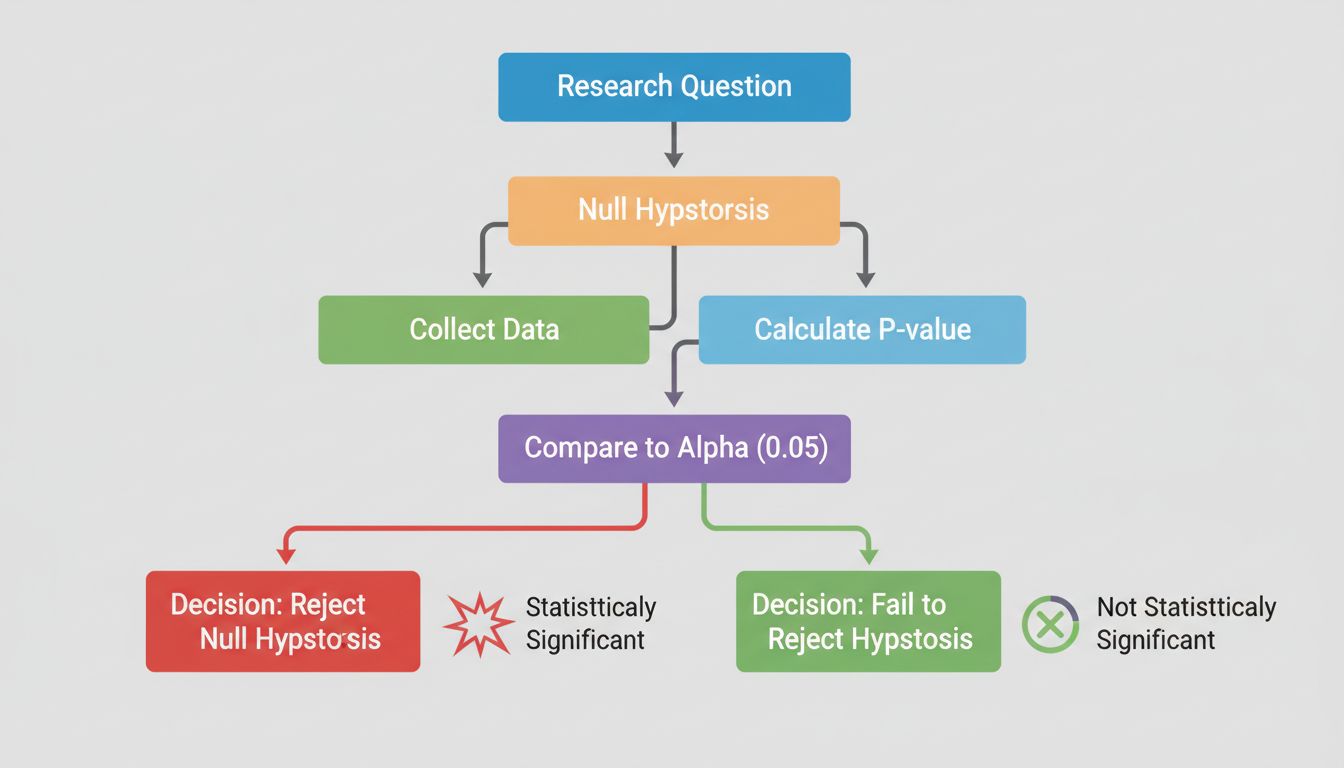
In het hart van statistische significantie ligt hypothesetoetsing, een gestructureerde methode voor het beoordelen van claims over uw data. Het proces begint met het formuleren van twee concurrerende hypotheses: de nulhypothese en de alternatieve hypothese. De nulhypothese gaat ervan uit dat er geen echt effect of verschil bestaat tussen de groepen die u bestudeert—het vertegenwoordigt in feite de status quo of de aanname dat elk waargenomen verschil puur door toeval komt. De alternatieve hypothese daarentegen stelt dat er wel degelijk een echt effect of verschil is.
Neem een praktisch voorbeeld: u test of een nieuwe affiliate marketingcampagne hogere conversieratio’s oplevert dan uw bestaande aanpak. Uw nulhypothese zou stellen dat beide campagnes identieke conversieratio’s opleveren, terwijl uw alternatieve hypothese zou beweren dat de nieuwe campagne anders presteert. De statistische toets beoordeelt vervolgens welke hypothese sterker door de data wordt ondersteund. Dit kader voorkomt dat onderzoekers en analisten alleen resultaten uitkiezen die hun verwachtingen bevestigen; in plaats daarvan vereist het dat zij bewijzen dat hun bevindingen onwaarschijnlijk door toeval zijn ontstaan.
Het mooie aan hypothesetoetsing is de objectiviteit. In plaats van op subjectief oordeel te vertrouwen, gebruikt u wiskundige berekeningen om te bepalen of uw data voldoende bewijs levert om de nulhypothese te verwerpen. Als het bewijs sterk genoeg is, kunt u met vertrouwen stellen dat uw geobserveerde effect statistisch significant is—oftewel, het is waarschijnlijk geen toevalstreffer.
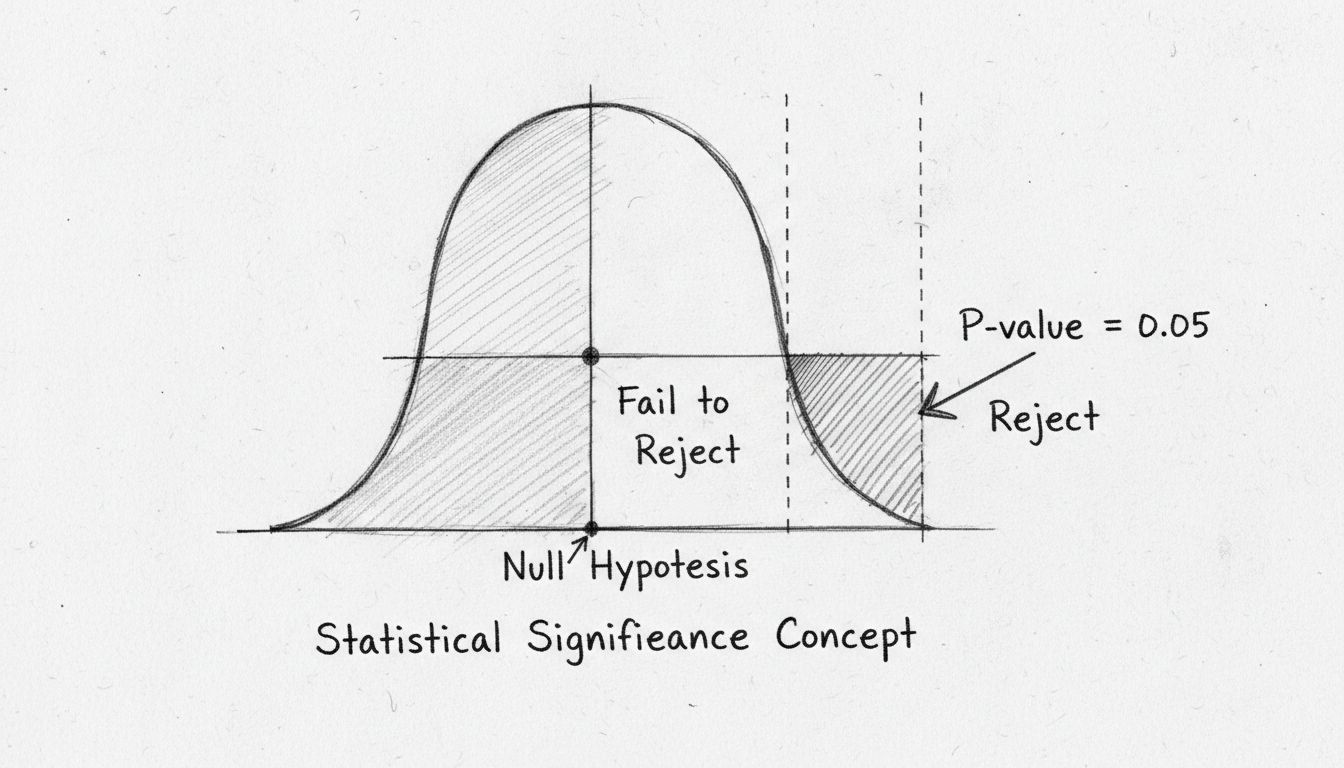
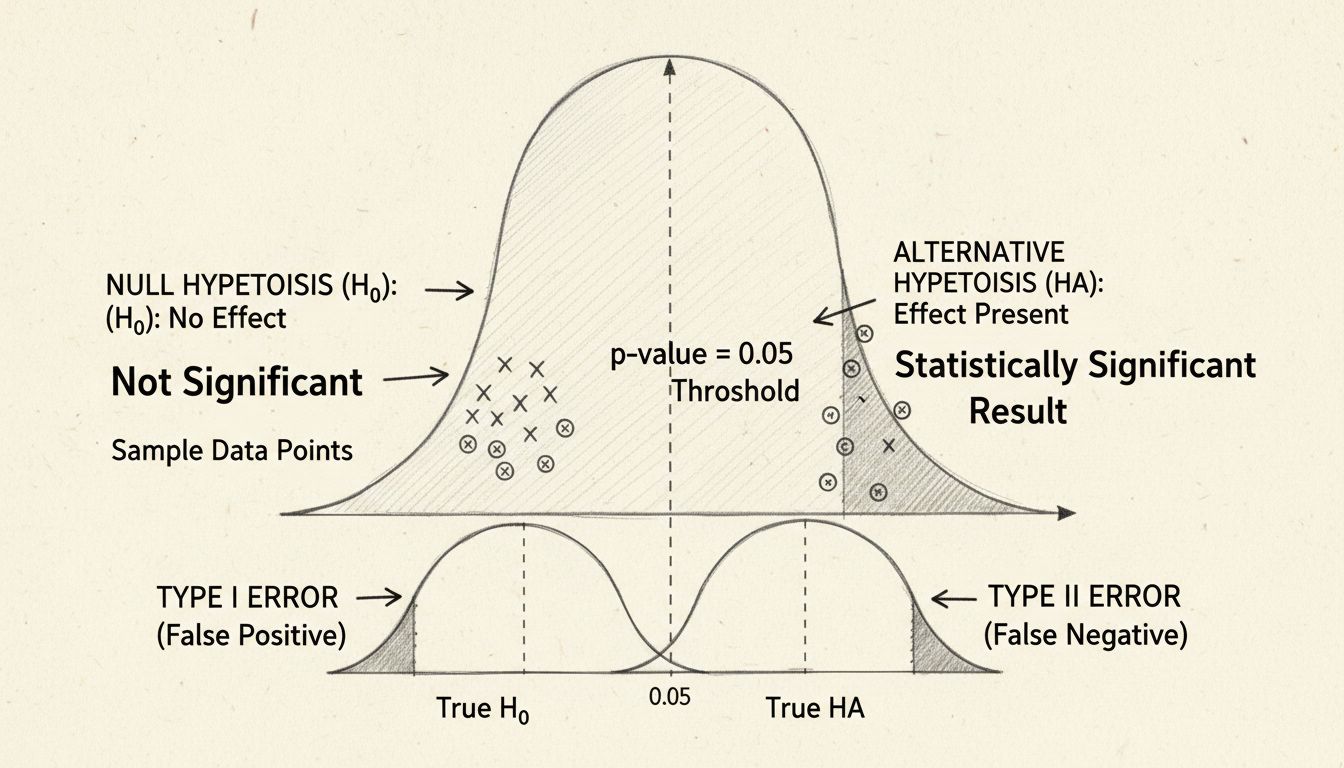
De p-waarde is waarschijnlijk de meest gebruikte maatstaf bij het testen van statistische significantie, maar wordt vaak verkeerd begrepen. De p-waarde geeft de kans weer dat u uw resultaten (of nog extremere resultaten) zou waarnemen als de nulhypothese daadwerkelijk waar is. Met andere woorden, het beantwoordt de vraag: “Hoe waarschijnlijk is het dat ik deze data zou zien als er echt geen effect is?” Een lage p-waarde geeft aan dat uw resultaten onder de nulhypothese zeer onwaarschijnlijk zijn, wat suggereert dat de nulhypothese waarschijnlijk onjuist is en uw effect echt.
De gangbare drempel voor statistische significantie is een p-waarde van 0,05 of lager, wat neerkomt op een kans van 5% dat uw resultaten door toeval zijn ontstaan. Dit betekent dat u bereid bent een risico van 5% te accepteren om de nulhypothese onterecht te verwerpen als deze eigenlijk waar is (Type I fout genoemd). Deze drempel is echter enigszins willekeurig en verschilt per vakgebied en context. In medisch onderzoek, waar de gevolgen van valse positieven groot kunnen zijn, wordt vaak een strengere drempel van 0,01 (1%) gehanteerd. Daarentegen kan in verkennend onderzoek of bij vroege tests een drempel van 0,10 (10%) acceptabel zijn.
| P-waarde bereik | Interpretatie | Typische actie |
|---|---|---|
| p < 0,01 | Zeer significant | Sterk bewijs tegen de nulhypothese |
| 0,01 ≤ p < 0,05 | Significant | Matig bewijs tegen de nulhypothese |
| 0,05 ≤ p < 0,10 | Marginaal significant | Zwak bewijs tegen de nulhypothese |
| p ≥ 0,10 | Niet significant | Onvoldoende bewijs om nulhypothese te verwerpen |
Het is cruciaal te begrijpen wat een p-waarde niet aangeeft. Een p-waarde van 0,03 betekent niet dat er 97% kans is dat uw hypothese waar is. Het geeft ook niet de grootte of praktische relevantie van uw effect aan. Een statistisch significant resultaat kan nog steeds een triviaal klein effect zijn zonder echte impact. Dit onderscheid tussen statistische significantie en praktische significantie is een van de meest voorkomende bronnen van verwarring in data-analyse.
Terwijl p-waarden aangeven of er een effect bestaat, geven betrouwbaarheidsintervallen cruciale informatie over de omvang en precisie van dat effect. Een betrouwbaarheidsinterval is een bereik van waarden dat waarschijnlijk de werkelijke effectgrootte bevat, berekend met een bepaald betrouwbaarheidsniveau (meestal 95%). Als u test of een nieuwe affiliateprogramma-functie de commissies verhoogt, kan een 95% betrouwbaarheidsinterval aangeven dat de werkelijke toename ergens tussen 2% en 8% ligt, met 95% zekerheid dat de echte waarde in dit bereik valt.
Betrouwbaarheidsintervallen bieden verschillende voordelen boven alleen p-waarden. Ten eerste laten ze zowel de richting als de omvang van een effect zien, waardoor u een completer beeld krijgt. Ten tweede helpen ze bij het beoordelen van praktische significantie—zelfs als een effect statistisch significant is, als het betrouwbaarheidsinterval aantoont dat het effect verwaarloosbaar klein is, is implementatie mogelijk niet zinvol. Ten derde geven smalle betrouwbaarheidsintervallen precieze schattingen aan, terwijl brede intervallen op meer onzekerheid wijzen.
Effectgrootte meet de sterkte van de relatie tussen variabelen of de omvang van het verschil tussen groepen. Veelgebruikte maten voor effectgrootte zijn onder andere Cohen’s d (voor het vergelijken van gemiddelden), correlatiecoëfficiënten en odds ratio’s. Een effect kan statistisch significant zijn maar een kleine effectgrootte hebben, wat betekent dat de praktische impact minimaal is. Omgekeerd kan een groot effect niet statistisch significant zijn als uw steekproef te klein is. Professionele analisten rapporteren altijd de effectgrootte naast p-waarden om een volledig beeld te geven van hun bevindingen.
Steekproefgrootte speelt een cruciale rol bij het bepalen van statistische significantie. Grotere steekproeven geven meer informatie over uw populatie en verkleinen het effect van willekeurige variatie, waardoor echte effecten makkelijker zijn te detecteren. Kleine steekproeven zijn daarentegen gevoeliger voor toevallige schommelingen, wat zowel tot valse positieven (een effect detecteren dat er niet is) als valse negatieven (een bestaand effect missen) kan leiden.
Het verband tussen steekproefgrootte en statistische power is fundamenteel in onderzoeksopzet. Statistische power is de kans dat u de nulhypothese correct verwerpt wanneer deze onjuist is—oftewel, uw vermogen om een echt effect te detecteren. De meeste onderzoekers streven naar een power van 0,80 (80%), wat betekent dat ze bereid zijn een kans van 20% te accepteren om een echt effect te missen. Om deze power te bereiken, heeft u een voldoende grote steekproef nodig, afhankelijk van de verwachte effectgrootte, het gekozen significantieniveau en het type statistische toets.
Voordat een studie of experiment wordt uitgevoerd, zouden onderzoekers een poweranalyse moeten uitvoeren om de benodigde steekproefgrootte te bepalen. Dit voorkomt dat middelen worden verspild aan te kleine studies waarin geen betekenisvolle effecten kunnen worden gevonden, maar ook dat onnodig grote studies te veel tijd en geld kosten. In de context van affiliate marketing betekent dit dat u moet bepalen hoeveel conversies of kliks u moet observeren voordat u met vertrouwen kunt concluderen dat een wijziging in de campagne daadwerkelijk impact heeft.
Verschillende onderzoeksvragen en datatypes vereisen verschillende statistische toetsen. De keuze voor een test hangt af van factoren zoals het aantal vergeleken groepen, of de data normaal verdeeld is, of steekproeven onafhankelijk of gepaard zijn, en het type uitkomstvariabele (continu, categorisch, enzovoorts).
De Student’s t-test vergelijkt de gemiddelden van twee groepen en is een van de meest gebruikte toetsen. Deze is geschikt wanneer u continue data heeft (zoals omzetbedragen) en wilt bepalen of twee groepen significant verschillen. De test houdt rekening met de variabiliteit binnen elke groep en de steekproefgroottes, en levert een t-waarde die wordt vergeleken met een kritieke waarde om significantie te bepalen.
De chi-kwadraattoets wordt gebruikt voor categorische data om te bepalen of waargenomen frequenties significant verschillen van verwachte frequenties. Als u bijvoorbeeld analyseert of het affiliatekanaal (e-mail, sociale media, display-advertenties) de conversieratio beïnvloedt, is een chi-kwadraattoets geschikt.
ANOVA (Analyse van Variantie) breidt de t-test uit naar het vergelijken van gemiddelden van drie of meer groepen tegelijk. Dit voorkomt het probleem van multiple comparisons, waarbij het uitvoeren van veel aparte toetsen de kans op valse positieven verhoogt.
De Mann-Whitney U-toets en Wilcoxon rangsomtoets zijn niet-parametrische alternatieven die worden gebruikt wanneer data niet voldoet aan de aannames van parametrische toetsen, bijvoorbeeld als de data niet normaal verdeeld is.
In het bedrijfsleven stuurt statistische significantie belangrijke beslissingen aan op talloze gebieden. Marketingteams gebruiken A/B-tests met statistische significantie om te bepalen of website-aanpassingen, onderwerpregels in e-mails of advertentiecreaties daadwerkelijk prestatiecijfers verbeteren. In plaats van te vertrouwen op onderbuikgevoelens of observaties op kleine schaal, stellen datagedreven bedrijven vooraf significantiedrempels vast voordat ze testen uitvoeren, zodat beslissingen worden genomen op basis van betrouwbaar bewijs.
Voor affiliate marketing helpt statistische significantie u te bepalen welke affiliates, campagnes en promotiestrategieën daadwerkelijk omzet genereren, en welke alleen succesvol lijken door toeval. Wanneer u beoordeelt of een nieuwe commissiestructuur de prestaties van affiliates verhoogt, voorkomt statistische toetsing dat u dure wijzigingen doorvoert op basis van kortetermijnschommelingen. Het geavanceerde analyticsplatform van PostAffiliatePro stelt u in staat affiliate-metrics te volgen met de statistische nauwkeurigheid die nodig is voor weloverwogen optimalisatiebeslissingen.
In farmaceutisch en medisch onderzoek bepaalt statistische significantie of nieuwe behandelingen effectief genoeg zijn om goedkeuring en gebruik te rechtvaardigen. Klinische studies moeten aantonen dat de voordelen van een medicijn statistisch significant zijn voordat het aan patiënten wordt voorgeschreven. De inzet is hoog, daarom worden in medisch onderzoek doorgaans strengere significantieniveaus gehanteerd dan in andere sectoren.
Een van de hardnekkigste misvattingen is dat statistische significantie causaliteit aantoont. Een statistisch significante correlatie tussen twee variabelen betekent niet dat de ene de oorzaak is van de andere. Het klassieke voorbeeld is de sterke correlatie tussen Nicolas Cage-films en verdrinkingen in zwembaden—overduidelijk veroorzaakt het een het ander niet. Statistische significantie geeft alleen aan dat een relatie onwaarschijnlijk door toeval is ontstaan; causaliteit vaststellen vereist aanvullend bewijs, zoals een logisch mechanisme, tijdsvolgorde en gecontroleerde experimenten.
Een andere veelgemaakte fout is p-hacking of data dredging, waarbij onderzoekers talloze statistische toetsen uitvoeren op dezelfde dataset tot ze significante resultaten vinden. Deze praktijk vergroot kunstmatig de kans op valse positieven, omdat u met genoeg toetsen altijd wel iets “significant” vindt puur door toeval. Als u 20 onafhankelijke toetsen uitvoert met een significantieniveau van 0,05, mag u verwachten dat er ongeveer één vals positief resultaat is puur door toeval. Verantwoorde onderzoekers specificeren hun hypotheses en statistische toetsen voorafgaand aan de analyse, om dit probleem te voorkomen.
Het verkeerd interpreteren van niet-significante resultaten is nog een valkuil. Een niet-significant resultaat bewijst niet dat er geen effect is; het betekent alleen dat u onvoldoende bewijs heeft om de nulhypothese te verwerpen. Dit kan komen door een te kleine steekproef, hoge variabiliteit in de data, of een daadwerkelijk afwezig effect. Het ontbreken van bewijs is geen bewijs van afwezigheid.
Het vakgebied statistiek blijft zich ontwikkelen, waarbij steeds meer aandacht is voor de beperkingen van traditionele p-waardebenaderingen. Veel statistici pleiten nu voor een genuanceerdere aanpak waarin p-waarden worden gecombineerd met effectgrootte, betrouwbaarheidsintervallen en Bayesiaanse methoden. Bayesiaanse statistiek, waarin eerdere kennis wordt verwerkt en overtuigingen worden bijgewerkt op basis van waargenomen data, biedt een alternatief kader dat sommigen intuïtiever en flexibeler vinden dan frequentistische benaderingen.
Sequentiële toetsen en adaptieve ontwerpen winnen aan populariteit, waardoor onderzoekers resultaten kunnen monitoren terwijl data binnenkomt en tussentijds besluiten kunnen nemen over het voortzetten, aanpassen of stoppen van studies. Deze aanpak is vooral waardevol in het bedrijfsleven, waar snel beslissingen moeten worden genomen. Tools zoals Statsig’s Stats Engine passen sequentiële toetsen toe met controle op het false discovery rate, wat snellere en nauwkeurigere besluitvorming tijdens experimenten mogelijk maakt.
De replicatiecrisis in de wetenschap heeft ook het belang aangetoond van een goed begrip van statistische significantie. Veel gepubliceerde bevindingen blijken niet te repliceren, deels omdat onderzoekers en tijdschriften te veel hebben gefocust op het behalen van statistische significantie en effectgrootte en praktische relevantie over het hoofd zagen. De nadruk verschuift dan ook naar transparantie, preregistratie van studies, en het rapporteren van alle resultaten, ongeacht significantie.
Om statistische significantie effectief te gebruiken, stelt u uw significantieniveau en steekproefgrootte vast voordat u uw analyse uitvoert. Dit voorkomt de verleiding om drempels aan te passen na het zien van de resultaten. Rapporteer altijd effectgrootte en betrouwbaarheidsintervallen naast p-waarden om een volledig beeld te geven van uw bevindingen. Overweeg de praktische relevantie van uw resultaten—een statistisch significant effect kan te klein zijn om in de praktijk van betekenis te zijn.
Wees transparant over uw methodologie, bijvoorbeeld over hoe u met ontbrekende data, uitbijters en multiple comparisons bent omgegaan. Als u meerdere toetsen uitvoerde, pas dan passende correcties toe, zoals de Bonferroni-correctie, om uw algehele significantieniveau te waarborgen. Documenteer uw analyseproces en wees bereid uw data en code te delen voor verificatie en replicatie.
Onthoud ten slotte dat statistische significantie een hulpmiddel is, geen einddoel. Het helpt u betere beslissingen te nemen door de invloed van toeval te verkleinen, maar het moet worden gecombineerd met domeinkennis, praktische overwegingen en zakelijk inzicht. In affiliate marketing helpt statistische significantie u te bepalen welke strategieën werkelijk prestaties verbeteren, maar u moet bij strategische beslissingen ook rekening houden met factoren als implementatiekosten, tevredenheid van affiliates en langetermijnduurzaamheid.
De geavanceerde analysetools en rapportages van PostAffiliatePro helpen u affiliateprestaties met statistische nauwkeurigheid te volgen. Begrijp welke campagnes echt resultaat opleveren en optimaliseer uw affiliateprogramma op basis van betrouwbare data-inzichten.
Statistische significantie drukt de betrouwbaarheid van gemeten gegevens uit, waardoor bedrijven echte effecten van toeval kunnen onderscheiden en weloverwogen ...
Ontdek waarom statistische significantie van belang is bij data-analyse, onderzoek en zakelijke beslissingen. Leer over p-waarden, hypothesetoetsing en hoe je r...
Beheers statistische significantie in A/B-testen voor betting affiliate campagnes.
Cookie Toestemming
We gebruiken cookies om uw browse-ervaring te verbeteren en ons verkeer te analyseren. See our privacy policy.